Модели авторегрессии скользящего среднего ARMA (p, q) для анализа временных рядов - часть 3

1. Байесовский информационный критерий
2. Байесовский информационный критерий
3. Тест Юнга-Бокса
4. Тест Юнга-Бокса
5. Autogressive Moving Average (ARMA) Модели порядка p, q
6. обоснование
7. Определение
8. Авторегрессионная скользящая средняя Модель порядка p, q
9. Симуляции и коррелограммы
10. Выбор лучшей модели ARMA (p, q)
11. Финансовые данные
12. Следующие шаги

Это третий и последний пост в мини-серии по моделям авторегрессионного скользящего среднего (ARMA) для анализа временных рядов. Мы ввели Авторегрессионные модели а также Скользящие средние модели в двух предыдущих статьях. Теперь пришло время объединить их для создания более сложной модели.

В конечном итоге это приведет нас к моделям ARIMA и GARCH, которые позволят нам прогнозировать доходность активов и прогнозировать волатильность. Эти модели станут основой для торговых сигналов и методов управления рисками.

Если вы читали Часть 1 а также Часть 2 вы увидите, что мы склонны следовать шаблону для нашего анализа модели временных рядов. Я кратко повторю здесь:

• Обоснование - Почему нас интересует именно эта модель?
• Определение - математическое определение, чтобы уменьшить двусмысленность.
• Коррелограмма - построение образца коррелограммы для визуализации поведения моделей.
• Моделирование и подгонка - Подгонка модели к моделированию, чтобы убедиться, что мы правильно поняли модель.
• Реальные финансовые данные - примените модель к реальным историческим ценам на активы.
• Предсказание - прогнозировать последующие значения для построения торговых сигналов или фильтров.

Чтобы следовать этой статье, рекомендуется взглянуть на предыдущие статьи по анализу временных рядов. Их все можно найти Вот ,

Байесовский информационный критерий

В Часть 1 этой серии статей мы рассматривали информационный критерий Акаике (AIC) как средство, помогающее нам выбирать между отдельными «лучшими» моделями временных рядов.

Тесно связанным инструментом является Байесовский информационный критерий (BIC). По сути, он имеет поведение, аналогичное AIC, в том, что он наказывает модели за слишком большое количество параметров. Это может привести к переобучения , Разница между BIC и AIC заключается в том, что BIC более строг с его штрафом за дополнительные параметры.

Байесовский информационный критерий

Если мы возьмем функция правдоподобия для статистической модели, которая имеет $ k $ параметров и $ L $ максимизирует вероятность тогда Байесовский информационный критерий определяется как:

\ begin {eqnarray} BIC = -2 \ text {log} (L) + k \ text {log} (n) \ end {eqnarray}

Где $ n $ - количество точек данных во временном ряду.

Мы будем использовать AIC и BIC ниже при выборе подходящих моделей ARMA (p, q).

Тест Юнга-Бокса

В Часть 1 этой серии статей Раджан упомянул в комментариях Disqus, что тест Льюнга-Бокса был более подходящим, чем использование критерия информации Акаике байесовского критерия информации при принятии решения о том, подходит ли модель ARMA для временного ряда.

Тест Льюнга-Бокса - это классический тест гипотезы, предназначенный для проверки того, существенно ли отличается набор автокорреляций модели согласованного временного ряда от нуля. Тест не проверяет каждую индивидуальную задержку на случайность, а проверяет случайность по группе лагов.

Формально:

Тест Юнга-Бокса

Мы определяем нулевую гипотезу $ {\ bf H_0} $ следующим образом: данные временных рядов в каждом лаге н.о.р. то есть корреляции между значениями ряда популяции равны нулю.

Мы определяем альтернативную гипотезу $ {\ bf H_a} $ как: Данные временного ряда не идентифицированы и обладают последовательной корреляцией.

Мы рассчитываем следующее тестовая статистика , $ Q $:

\ begin {eqnarray} Q = n (n + 2) \ sum_ {k = 1} ^ {h} \ frac {\ hat {\ rho} ^ 2_k} {nk} \ end {eqnarray}

Где $ n $ - длина выборки временного ряда, $ \ hat {\ rho} _k $ - автокорреляция выборки при лаге $ k $, а $ h $ - количество лагов в тесте.

Правило принятия решения о том, следует ли отклонять нулевую гипотезу $ {\ bf H_0} $, заключается в проверке, является ли $ Q> \ chi ^ 2 _ {\ alpha, h} $ для распределение хи-квадрат с $ h $ степенями свободы в $ 100 (1-альфа) $ -ом процентиле.

Хотя детали теста могут показаться немного сложными, на самом деле мы можем использовать R для вычисления теста для нас, что несколько упрощает процедуру.

Autogressive Moving Average (ARMA) Модели порядка p, q

Теперь, когда мы обсудили BIC и тест Льюнга-Бокса, мы готовы обсудить нашу первую смешанную модель, а именно авторегрессионную скользящую среднюю порядка p, q или ARMA (p, q).

обоснование

На сегодняшний день мы рассмотрели процессы авторегрессии и процессы скользящего среднего.

Первая модель рассматривает свое поведение в прошлом как исходные данные для модели и как таковые пытается отразить эффекты участников рынка, такие как импульс и возврат к среднему значению в торговле акциями.

Последняя модель используется для характеристики «шоковой» информации для ряда, такой как неожиданное объявление о доходах или неожиданное событие (например, Разлив нефти BP Deepwater Horizon ).

Следовательно, модель ARMA пытается охватить оба эти аспекта при моделировании финансовых временных рядов.

Обратите внимание, что модель ARMA не учитывает кластеризацию волатильности, ключевой эмпирический феномен многих финансовых временных рядов. Это не условно гетероскедастическая модель. Для этого нам нужно дождаться моделей ARCH и GARCH.

Определение

Модель ARMA (p, q) представляет собой линейную комбинацию двух линейных моделей и, таким образом, сама по-прежнему линейна:

Авторегрессионная скользящая средняя Модель порядка p, q

Модель временного ряда, $ \ {x_t \} $, является моделью авторегрессии скользящего среднего порядка $ p, q $ , ARMA (p, q), если:

\ begin {eqnarray} x_t = \ alpha_1 x_ {t-1} + \ alpha_2 x_ {t-2} + \ ldots + w_t + \ beta_1 w_ {t-1} + \ beta_2 w_ {t-2} \ ldots + \ beta_q w_ {tq} \ end {eqnarray}

Где $ \ {w_t \} $ белый шум с $ E (w_t) = 0 $ и дисперсией $ \ sigma ^ 2 $.

Если мы рассмотрим оператор обратного сдвига , $ {\ bf B} $ (см. предыдущая статья ) тогда мы можем переписать вышесказанное как функцию $ \ theta $ и $ \ phi $ из $ {\ bf B} $:

\ begin {eqnarray} \ theta_p ({\ bf B}) x_t = \ phi_q ({\ bf B}) w_t \ end {eqnarray}

Мы можем прямо видеть, что, устанавливая $ p \ neq 0 $ и $ q = 0 $, мы восстанавливаем модель AR (p). Аналогично, если мы установим $ p = 0 $ и $ q \ neq 0 $, мы восстановим модель MA (q).

Одной из ключевых особенностей модели ARMA является то, что она экономна и избыточна по своим параметрам. То есть модель ARMA часто требует меньше параметров, чем модель AR (p) или MA (q). Кроме того, если мы переписываем уравнение в терминах BSO, то многочлены $ \ theta $ и $ \ phi $ могут иногда иметь общий множитель, что приводит к упрощению модели.

Симуляции и коррелограммы

Как и в случае с моделями авторегрессии и скользящего среднего, теперь мы будем моделировать различные серии ARMA, а затем попытаемся приспособить модели ARMA к этим реализациям. Мы выполняем это, потому что хотим убедиться, что понимаем процедуру подбора, включая способ вычисления доверительных интервалов для моделей, а также гарантируем, что процедура действительно восстанавливает разумные оценки для исходных параметров ARMA.

В части 1 и части 2 мы вручную построили серии AR и MA, вытащив выборки $ N $ из нормального распределения, а затем обработав конкретную модель временных рядов, используя лаги этих выборок.

Однако существует более простой способ имитации данных AR, MA, ARMA и даже ARIMA, просто используя метод arima.sim в R.

Давайте начнем с самой простой из возможных нетривиальных моделей ARMA, а именно модели ARMA (1,1). То есть авторегрессионная модель первого порядка в сочетании с моделью скользящего среднего первого порядка. Такая модель имеет только два коэффициента, $ \ alpha $ и $ \ beta $, которые представляют первые лаги самого временного ряда и «ударных» членов белого шума. Такая модель задается:

\ begin {eqnarray} x_t = \ alpha x_ {t-1} + w_t + \ beta w_ {t-1} \ end {eqnarray}

Нам нужно указать коэффициенты до моделирования. Давайте возьмем $ \ alpha = 0.5 $ и $ \ beta = -0.5 $:

> set.seed (1)> x сюжет (x)

Вывод следующий:

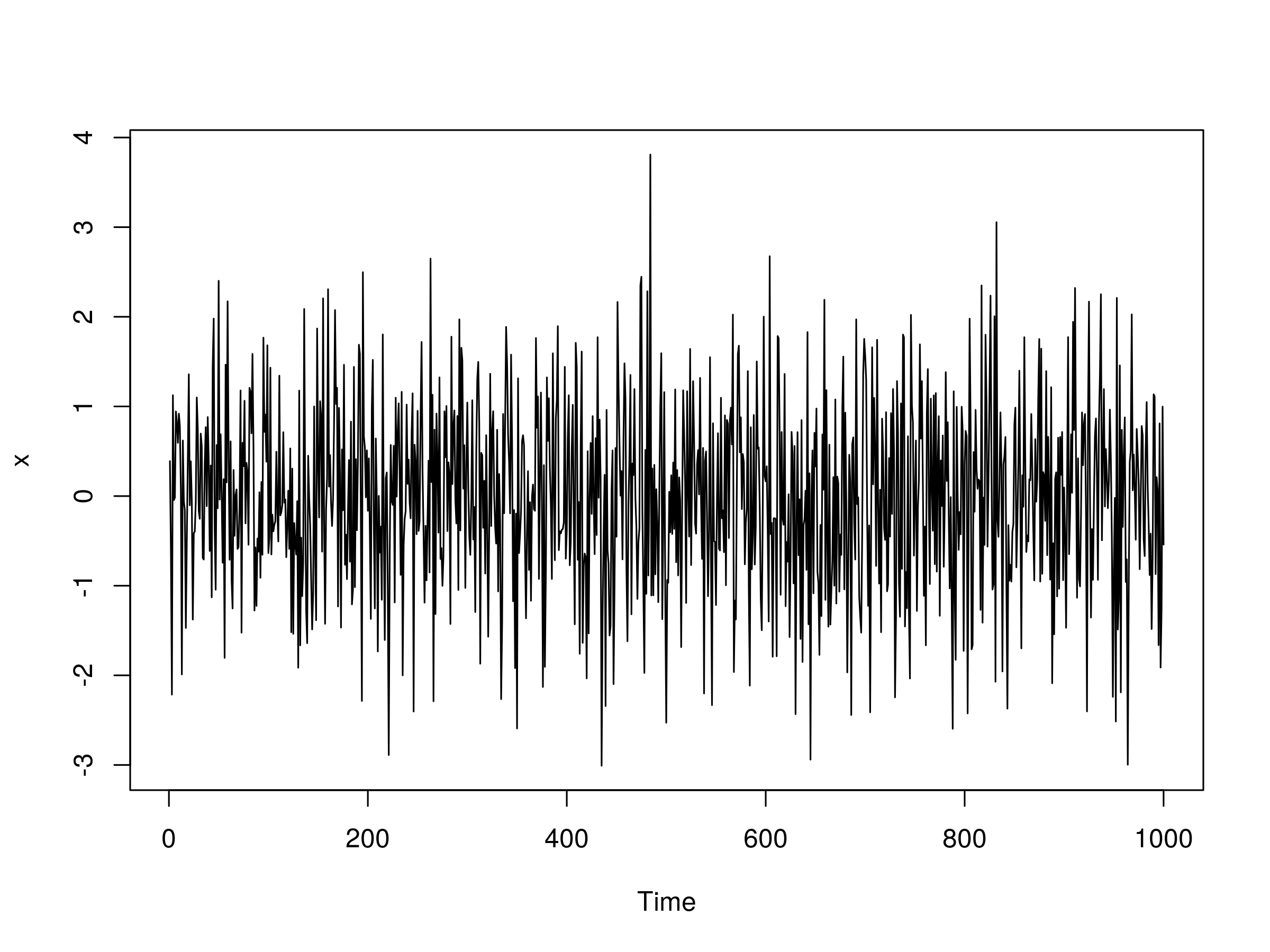Реализация модели ARMA (1,1), с $ \ alpha = 0,5 $ и $ \ beta = 0,5 $

Давайте также построим коррелограмму:

> acf (x)

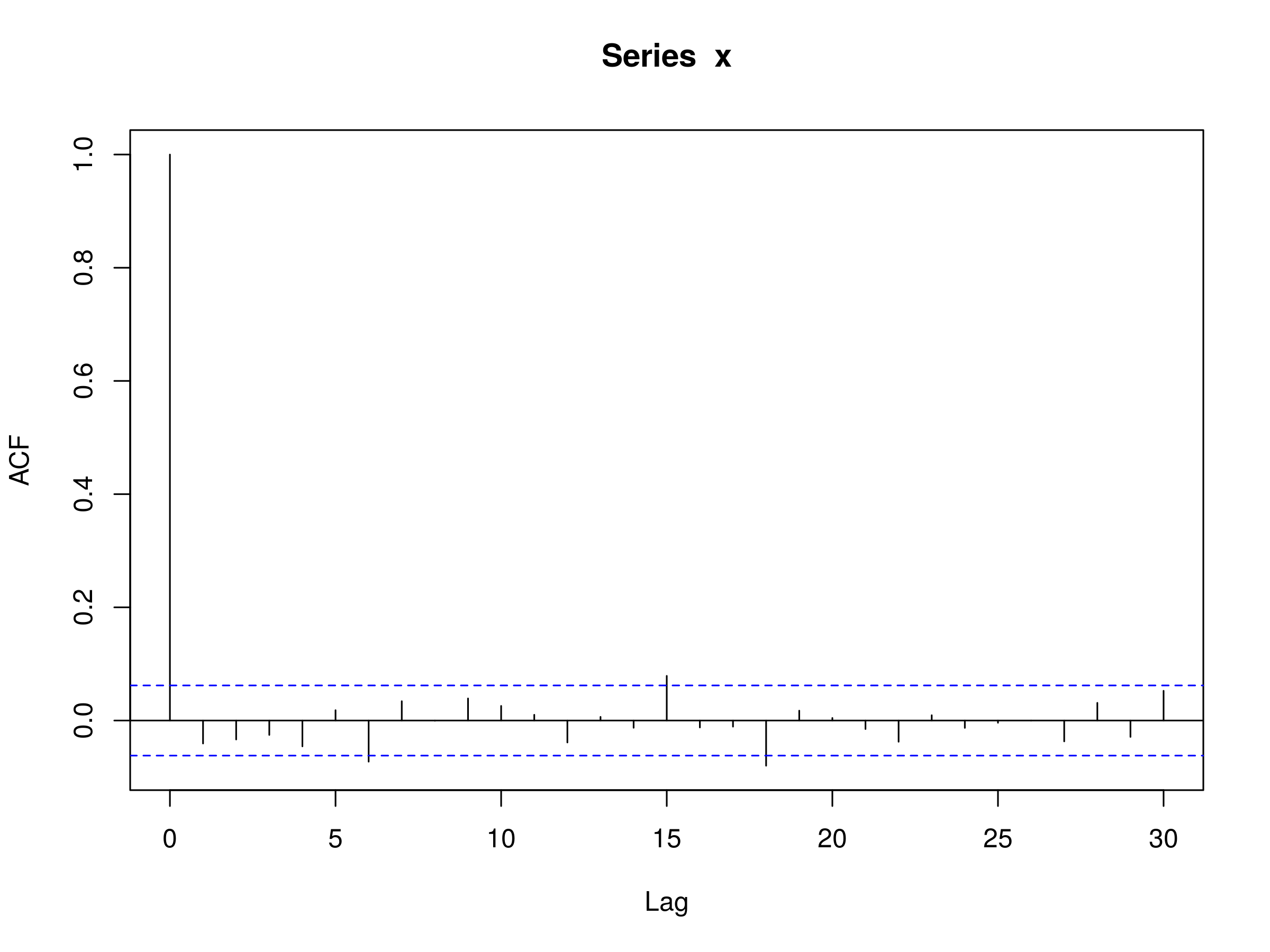Коррелограмма модели ARMA (1,1), с $ \ alpha = 0,5 $ и $ \ beta = 0,5 $

Мы можем видеть, что нет существенной автокорреляции, чего следует ожидать от модели ARMA (1,1).

Наконец, давайте попробуем определить коэффициенты и их стандартные ошибки, используя функцию arima:

> arima (x, order = c (1, 0, 1)) Вызов: arima (x = x, order = c (1, 0, 1)) Коэффициенты: ar1 ma1 intercept -0.3957 0.4503 0.0538 se 0.3727 0.3617 0.0337 sigma ^ 2 оценивается как 1,053: логарифмическая правдоподобие = -1444,79, aic = 2897,58

Мы можем рассчитать доверительные интервалы для каждого параметра, используя стандартные ошибки:

> -0,396 + с (-1,96, 1,96) * 0,373 [1] -1,12708 0,33508> 0,450 + с (-1,96, 1,96) * 0,362 [1] -0,25952 1,15952

Доверительные интервалы содержат истинные значения параметров для обоих случаев, однако следует отметить, что 95% доверительные интервалы очень широки (следствие достаточно больших стандартных ошибок).

Давайте теперь попробуем модель ARMA (2,2). То есть модель AR (2) в сочетании с моделью MA (2). Нам нужно указать четыре параметра для этой модели: $ \ alpha_1 $, $ \ alpha_2 $, $ \ beta_1 $ и $ \ beta_2 $. Давайте возьмем $ \ alpha_1 = 0.5 $, $ \ alpha_2 = -0.25 $ $ \ beta_1 = 0.5 $ и $ \ beta_2 = -0.3 $:

> set.seed (1)> x сюжет (x)

Выход нашей модели ARMA (2,2) выглядит следующим образом:

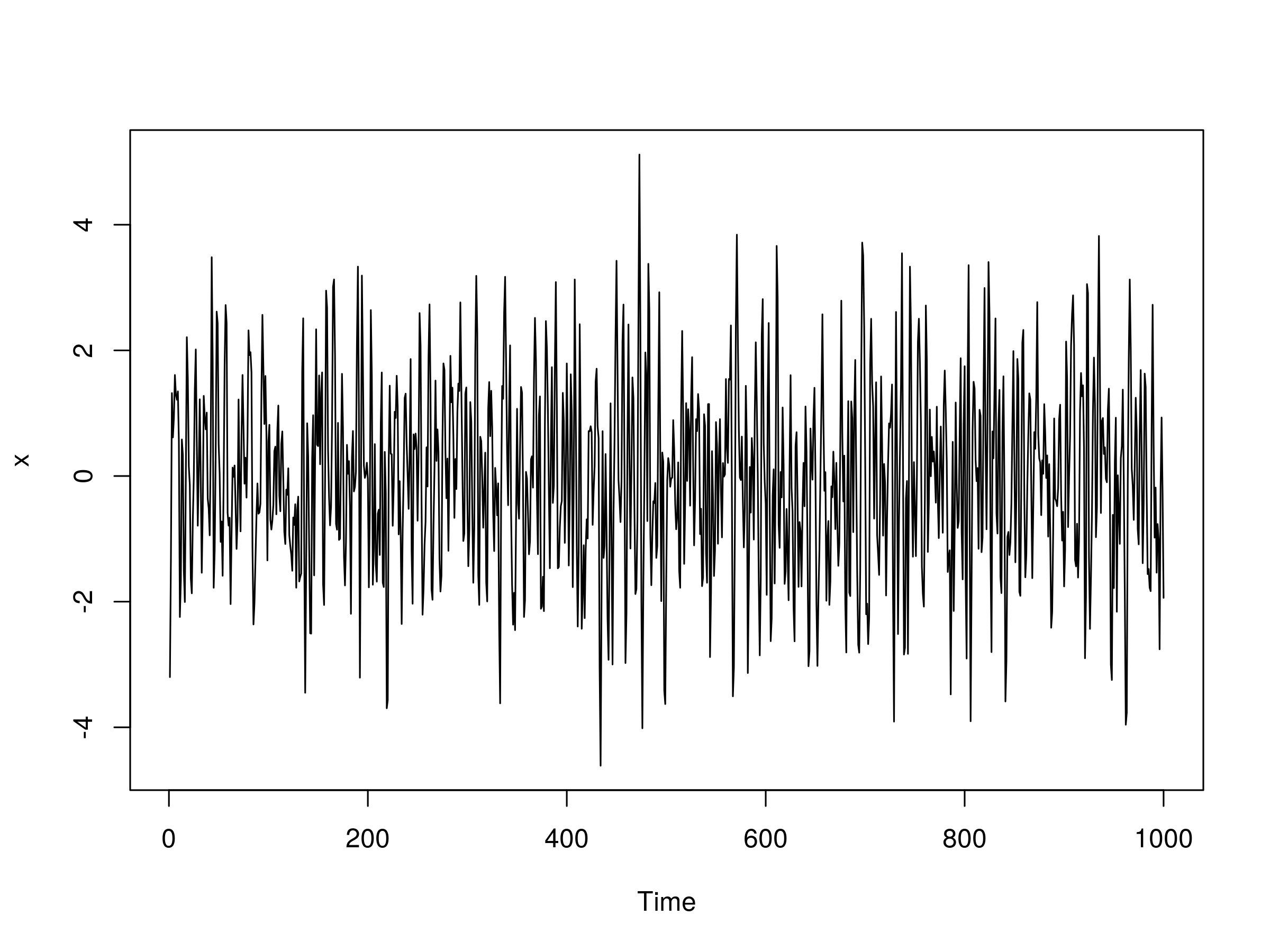Реализация модели ARMA (2,2), с $ \ alpha_1 = 0.5 $, $ \ alpha_2 = -0.25 $, $ \ beta_1 = 0.5 $ и $ \ beta_2 = -0.3 $

И соответствующая автокорреляция:

> acf (x)

Коррелограмма модели ARMA (2,2), с $ \ alpha_1 = 0,5 $, $ \ alpha_2 = -0,25 $, $ \ beta_1 = 0,5 $ и $ \ beta_2 = -0,3 $

Теперь мы можем попытаться приспособить модель ARMA (2,2) к данным:

> arima (x, order = c (2, 0, 2)) Вызов: arima (x = x, order = c (2, 0, 2)) Коэффициенты: ar1 ar2 ma1 ma2 перехват 0,6529 -0,2291 0,3191 -0,5522 -0,0290 se 0,0802 0,0346 0,0792 0,0771 0,0434 сигма ^ 2 оценивается как 1,06: логарифмическая правдоподобие = -1449,16, aic = 2910,32

Мы также можем рассчитать доверительные интервалы для каждого параметра:

> 0,653 + с (-1,96, 1,96) * 0,0802 [1] 0,495808 0,810192> -0,229 + с (-1,96, 1,96) * 0,0346 [1] -0,296816 -0,161184> 0,319 + с (-1,96, 1,96) * 0,0792 [ 1] 0,163768 0,474232> -0,552 + с (-1,96, 1,96) * 0,0771 [1] -0,703116 -0,400884

Обратите внимание, что доверительные интервалы для коэффициентов для компонента скользящего среднего ($ \ beta_1 $ и $ \ beta_2 $) на самом деле не содержат исходного значения параметра. Это подчеркивает опасность попытки подгонки моделей к данным, даже когда мы знаем истинные значения параметров!

Однако для торговых целей нам просто необходимо иметь прогнозирующую силу, которая превосходит случайность и дает достаточную прибыль сверх трансакционных издержек, чтобы быть прибыльной в долгосрочной перспективе.

Теперь, когда мы увидели несколько примеров смоделированных моделей ARMA, нам нужен механизм для выбора значений $ p $ и $ q $ при подгонке моделей к реальным финансовым данным.

Выбор лучшей модели ARMA (p, q)

Чтобы определить, какой порядок $ p, q $ модели ARMA подходит для ряда, нам нужно использовать AIC (или BIC) для подмножества значений для $ p, q $, а затем применить блок Юнга-Бокса. тест, чтобы определить, была ли достигнута хорошая подгонка для конкретных значений $ p, q $ .

Чтобы показать этот метод, мы собираемся сначала смоделировать конкретный процесс ARMA (p, q). Затем мы зациклим все попарные значения $ p \ in \ {0,1,2,3,4 \} $ и $ q \ in \ {0,1,2,3,4 \} $ и вычислим AIC , Мы выберем модель с самым низким значением AIC, а затем проведем тест Льюнга-Бокса на остатки, чтобы определить, насколько мы достигли хорошей подгонки.

Начнем с моделирования серии ARMA (3,2):

> set.seed (3)> x
Теперь мы создадим объект final для хранения наилучшего соответствия модели и минимального значения AIC. Мы перебираем различные комбинации $ p, q $ и используем текущий объект для хранения соответствия модели ARMA (i, j) для циклических переменных $ i $ и $ j $.
Если текущий AIC меньше, чем любой ранее рассчитанный AIC, мы устанавливаем конечный AIC на это текущее значение и выбираем этот порядок. После завершения цикла у нас есть порядок модели ARMA, сохраненный в final.order, и ARIMA (p, d, q) подгоняется (с интегрированным $ d $ компонентом, установленным в 0), сохраненным как final.arma: > final.aic final.order для (я в 0: 4) для (j в 0: 4) {> current.aic if (current.aic final.aic final.order final.arma}>}
Выведем коэффициенты AIC, order и ARIMA:> final.aic [1] 2863.365> final.order [1] 3 0 2> final.arma Вызов: arima (x = x, order = final.order) Коэффициенты: ar1 ar2 ar3 ma1 ma2 перехват 0,4470 -0,2822 0,4079 0,5519 -0,2367 0,0274 se 0,0867 0,0345 0,0309 0,0954 0,0905 0,0975 сигма ^ 2, оценивается как 1,009: логарифмическая правдоподобие = -1424,68, aic = 2863,36
Мы можем видеть, что первоначальный порядок моделируемой модели ARMA был восстановлен, а именно с $ p = 3 $ и $ q = 2 $. Мы можем нанести на график corelogram остатков модели, чтобы увидеть, выглядят ли они как реализация дискретного белого шума (DWN):> acf (остаток (final.arma))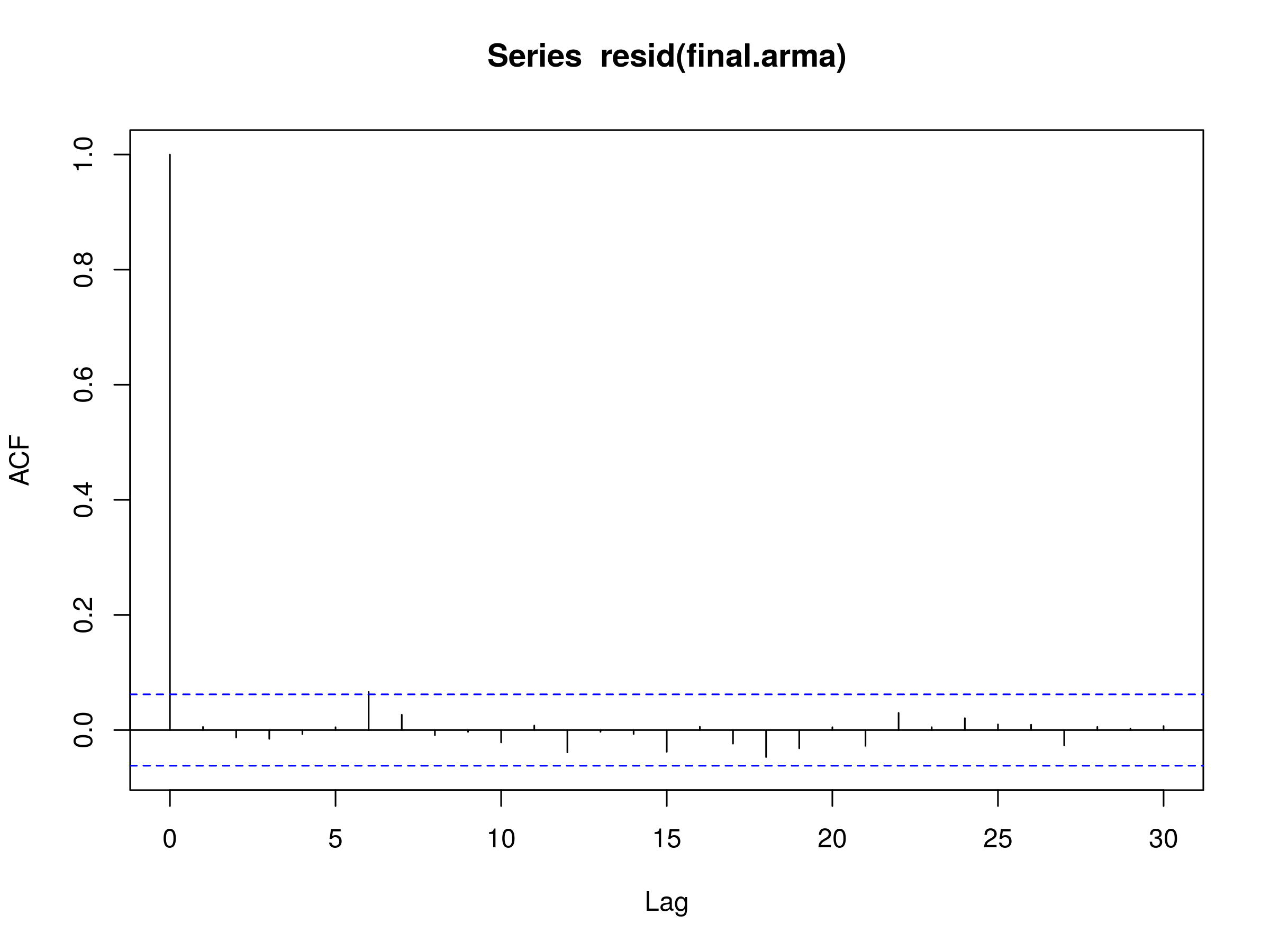
Коррелограмма невязок наилучшей модели ARMA (p, q), $ p = 3 $ и $ q = 2 $
Corelogram действительно выглядит как реализация DWN. Наконец, мы выполняем тест Льюнга-Бокса для 20 лагов, чтобы подтвердить это:> Box.test (остаток (final.arma), лаг = 20, тип = "Ljung-Box") Данные теста Box-Ljung: Остаток (окончательный. arma) X-квадрат = 13.1927, df = 20, значение p = 0,869
Обратите внимание, что значение p больше 0,05, что говорит о том, что остатки независимы на уровне 95%, и, таким образом, модель ARMA (3,2) обеспечивает хорошее соответствие модели.
Очевидно, что так и должно быть, поскольку мы сами симулировали данные! Однако именно эту процедуру мы будем использовать, когда подойдем для подгонки моделей ARMA (p, q) к индексу S & P500 в следующем разделе.

Финансовые данные

Теперь, когда мы наметили процедуру выбора оптимальной модели временных рядов для моделируемого ряда, применить ее к финансовым данным довольно просто. Для этого примера мы собираемся еще раз выбрать индекс акций США S & P500.
Давайте загрузим дневные цены закрытия, используя quantmod а затем создайте поток возврата журнала:> require (quantmod)> getSymbols ("^ GSPC")> sp = diff (log (Cl (GSPC)))
Давайте выполним ту же процедуру подгонки, что и для моделируемой серии ARMA (3,2), приведенной выше, в журнале возвращает серии S & P500, используя AIC:> spfinal.aic spfinal.order для (i в 0: 4) для (j в 0 : 4) {> spcurrent.aic if (spcurrent.aic spfinal.aic spfinal.order spfinal.arma}>}
Наилучшая модель имеет заказ ARMA (3,3):> spfinal.order [1] 3 0 3
Построим остатки подобранной модели в потоке ежедневных возвратов журнала S & P500:> acf (остаток (spfinal.arma), na.action = na.omit)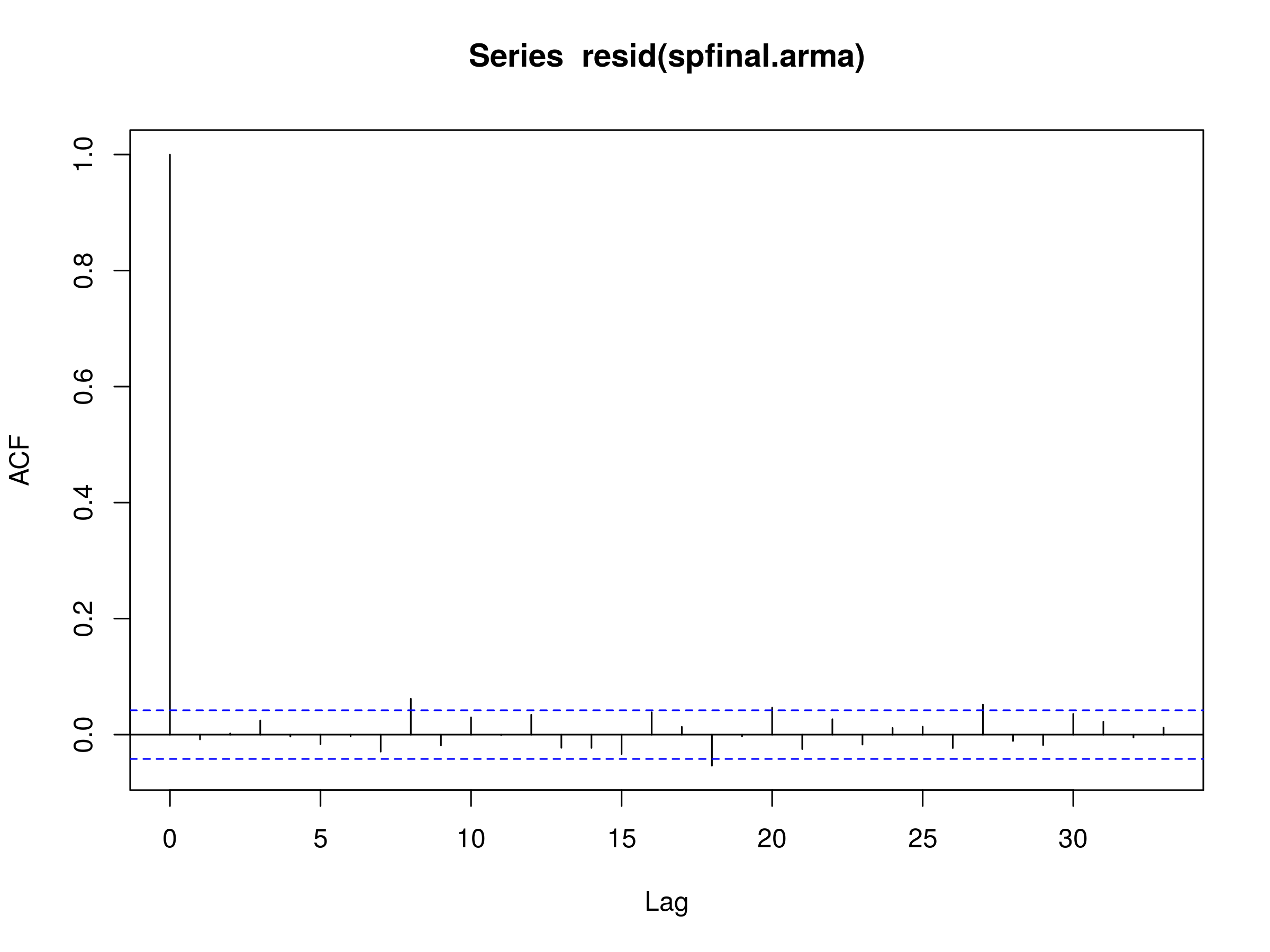
Коррелограмма невязок наилучшей модели ARMA (p, q), $ p = 3 $ и $ q = 3 $, в поток ежедневных журналов S & P500
Обратите внимание, что есть некоторые значительные пики, особенно при более высоких лагах. Это свидетельствует о плохой посадке. Давайте выполним тест Льюнга-Бокса, чтобы увидеть, есть ли у нас статистические доказательства этого:> Box.test (Остаток (spfinal.arma), lag = 20, type = "Ljung-Box") Данные теста Бокс-Льюнга: Остаток (spfinal .arma) X-квадрат = 37,1912, df = 20, значение p = 0,0111.
Как мы и предполагали, значение p меньше 0,05, и поэтому мы не можем сказать, что остатки являются реализацией дискретного белого шума. Следовательно, существует дополнительная автокорреляция в остатках, которая не объясняется подобранной моделью ARMA (3,3).

Следующие шаги

Как мы уже обсуждали в этой серии статей, мы видели признаки условной гетероскедастичности (кластеризации волатильности) в серии S & P500, особенно в периоды около 2007-2008 гг. Когда мы будем использовать модель GARCH позже в серии статей, мы увидим, как устранить эти автокорреляции.
На практике модели ARMA, как правило, никогда не подходят для возврата логарифмических акций. Нужно учитывать условную гетероскедастичность и использовать комбинацию ARIMA и GARCH. Следующая статья рассмотрит ARIMA и покажет, как «интегрированный» компонент отличается от модели ARMA, которую мы рассматривали в этой статье.

Похожие

Комментарии